鳩の巣原理のお話 ～作れないけれど、絶対にある！～
皆さんこんにちは。東進衛星予備校 金沢南校の北川と申します。
今月は、高校数学の問題でもよく使われる「鳩の巣原理」について紹介していきます。後半まで数式は出てこないので、「数学の話題はちょっと……」という人でも理解しやすい内容になっていると思います。是非お楽しみください。
目次
1.意味は簡単、鳩の巣原理
さて、本題に入ってきましょう。この記事を開いた時に、「鳩の巣原理」という言葉をまだ知らなかった人もそれなりにいると思います。ですから、まず、これが何なのかという話から始めなくてはいけません。
「鳩の巣原理」というのは「ある種類の数学の問題を解く時に使う、考え方の1つ」です。考え方、発想の方法に名前がついているわけですね。
そして、その考え方の中身というのも、決して難しいものではありません。例えば、以下のような状況を考えてみましょう。
あなたは友人の家にやってきました。友人は生活の癒しにと、鳩をたくさん飼っており、あなたもその恩恵にあずかろうと考えたわけです。
玄関に着くと、友人は歓待してくれました。すぐにリビングに通され、あなたはしばらく待つことに。ふと壁を見れば、鳩用のものであろう巣箱が5個、キレイに掛かっておりました。
鳩たちは眠っているのか巣箱から出てこず、中にいる鳩の様子は見えません。もしかしたら鳩が入っていない巣箱もあるのかもしれませんが、それすらも分かりません。リビングには他に鳩がいそうな場所は一切ありませんでした。
そうこうしているうちに、友人が返ってきました。
「やあ、鳩を飼っている割にはずいぶん静かだね。一体何羽飼っているんだい？」
友人は、あなたが鳩の話題に触れたのが嬉しかったのか、ニコニコしながら答えます。
「ああ、今はみんな寝てるんだが。全部で6羽の鳩を飼ってるんだよ」
あなたはそれを聞き、とっさに次のように返しました。
「えっ、そうなのかい。ぎゅうぎゅう詰めになっている鳩がいると思うけど、大丈夫なの？」
さて、上記の下手な小芝居にお付き合いいただきありがとうございました。実は、この文章こそが、端的に鳩の巣原理という考え方を示したものになっています。
数学の話なんてどこにも出てきていないのに？ と不思議に思われる方もいることでしょう。ポイントになるのは最後の一文「ぎゅうぎゅう詰めになっている鳩がいると思うけど、大丈夫なの？」というところになります。ちゃんと上記の文章を読んだ方なら、ここで文章中の聞き手が疑問に思っていることに同意できるのではないでしょうか。つまり、「ぎゅうぎゅう詰め[1]になっている巣箱がある」ということに納得できると思います。
なぜならば、巣箱は5個しかないのに、鳩は6羽いるわけですから、鳩の方が巣箱より多いのです。だから、鳩たちの様子を直接観察せずとも、（巣箱に全部の鳩が入っているならば）どれかの巣箱はぎゅうぎゅう詰めになっていると判断できるわけですね。
この直感を持ったうえで、もう少ししっかりと[2]鳩の巣原理の内容を述べるならばこうです。
A匹の鳩が、B個の巣箱に入っているとする。Aの方がBより大きい時、必ず2匹以上鳩が入っている巣箱が少なくとも1つは存在する。
少し注意点を述べておきましょう。
・すべての巣箱に1匹以上鳩が入っている必要はない。鳩が1匹も入っていない巣箱があっても良いものとする。
・2匹以上入っている巣箱は1個だけとは限らない。複数の巣箱に2匹以上入っていることもある。
[1] ここでの「ぎゅうぎゅう詰め」の定義は「1つの巣箱の中に2匹以上の鳩が入っている状態」を指すものとします
[2] 「厳密な」ではありません。厳密にやるなら集合と写像を定義して、単射を定義しないといけなくなるので……。
2.めっちゃスゴいぞ、鳩の巣原理
さて、こんな当たり前のことを考えて何が面白いのか、という話ですが……。
例えば有名な問題の1つにこんなものがあります（昔同じ趣旨の問題が神戸大学で出題されたことがあります）。
相異なる4つの正の整数からなるどのような集合であっても、そのうち適当な2つの要素を選んで差を取れば3で割り切れることを示せ。
何やらよく分からない、という人もいると思いますから、具体例を出してみましょう。
まず、何でもいいので適当に4つ、正の整数を思い浮かべてください（同じ数字を2つ思い浮かべる）。本当に何でも良いのですが、今回は3,20,47,91という4つが思い浮かんだとしましょう。
次に、今思浮かべた4つの数の中から、2つの数を選びます。3,20,47,91の中から、例えば3と20を選んだとしましょう。選んだ2つの数のうち大きい方から小さい方を引いてみましょう。20-3=17になります。
この調子で、「あり得る全部の数字のペア」をすべて探してきて引き算してみましょう。数は4つですから（順番を無視すると）、全部で6つのペアが考えられます。
$$20-3=17$$
$$47-3=44$$
$$91-3=88$$
$$47-20=27$$
$$91-20=71$$
$$91-47=44$$
そして、この足し算の結果をじーっと眺めて、「この引き算した結果の中に3で割り切れるものはあるだろうか？」と考えます。
実際にやってみれば分かることですが、今回は27が3で割り切れます。
引き算の結果が3で割り切れたのは偶然でしょうか？ 別の4つの数の組み合わせでも試してみましょう。
例えば4,22,31,86だったら？ この時は22-4=18が3で割り切れます。
じゃあ、80,112,193,421だったら？ この時も421-193=228が3で割り切れます。
他には？ 皆さんも好きな4つの数字を選んで考えてみてください。たぶん、6つできる数字のペアのうち、引き算した答えが3で割り切れるものが1つはあるはずです。
つまり、先ほどの問題の意味というのは
「どんな（バラバラの）4つの正の整数が思い浮かんだとしても、そのうち上手い2つを選んで大きい方から小さい方を引くと、必ずその答えが3で割り切れる」ということを証明しなさい
と、こんなものだったわけです。
それで、これはどうやったら証明できるのでしょう？
正の整数は無限にありますから、4つの数字の組み合わせを全部確かめる、という力技を取ることはできません。
ここでポイントとなるのが、先ほど紹介した「鳩の巣原理」です。
鳩の巣原理は、喩えのために鳩と巣箱を使っただけに過ぎません。鳩と見なせる何かが、巣箱と見なせる何かに分けられるときであれば、いつでも使えます。
具体的に見てみることにしましょう。鳩の巣原理をどう使ったのかが分かりやすいように、発想の根本ではなくて、答えから天下り式に解説していきます。
今回は、4つの正の整数を、3で割った余り別に分ける、ということを考えます。
これは、「思い浮かべた正の整数」という4つの「鳩」を、「3で割って割り切れる数を入れる箱」「3で割って1余る数を入れる箱」「3で割って2余る数を入れる箱」という3つの「巣箱」に入れていることになります。
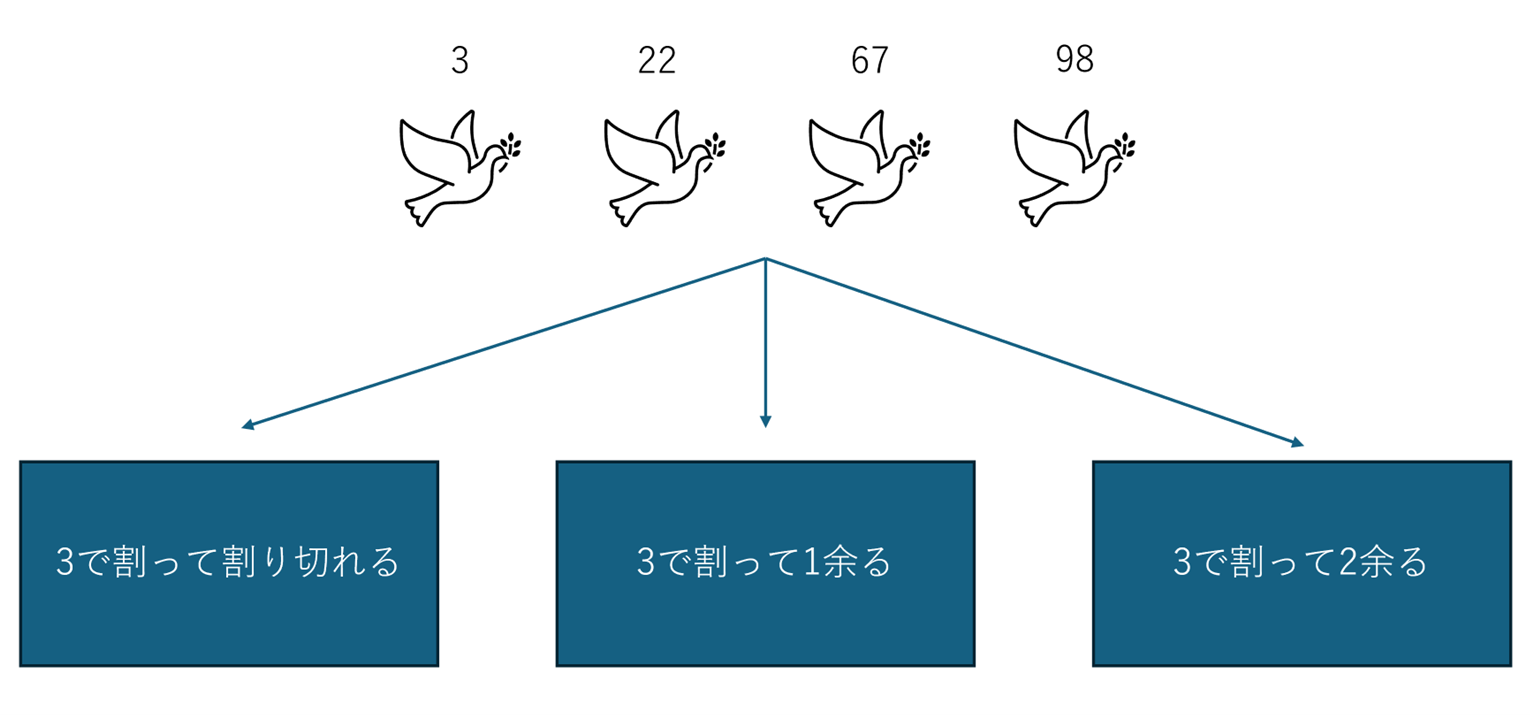
図:鳩が巣箱に割り振られている様子
さて、鳩の巣原理の主張を思い出してみると、鳩の数が巣箱の数より多い時には、2匹上鳩が入っている巣箱が1つ以上あるのでした。
つまり、今回で言えば「3で割って割り切れる」「3で割って1余る」「3で割って2余る」のどれかの箱には、2匹以上の鳩……2つ以上の整数が入っていることになります。
そして、同じ箱に入っている2つの整数は、3で割った余りが同じです。3で割った余りが同じであるような2つの整数を引き算すると、結果はどうなるでしょうか？
例えば、11と17は両方とも3で割った余りが2です。そして、17-11=6ですから、この結果は3で割り切れます。或いは、64と79は両方とも3で割った余りが1ですが、引き算の結果は79-64=15なので、3で割り切れます。
一般に、3で割った余りが等しい2つの整数を引き算すると3で割り切れることが以下のように証明できます（文字と数式が出てくる上に本質部分でもないので、気になる人以外は読み飛ばしてください）。
任意の正の整数は、非負整数 と2以下の非負整数 を用いて、 \(3n+r\)と書くことができる。
ここで、非負整数n,m(n≧m)と2以下の非負整数rを用いて、\(3n+r\)、\(3m+r\)と書ける2つの正の整数をとる。このとき、\((3n+r)-(3m+r)=3(n-m)\)であるが、これはこの2数の差が3で割れることを示している。
ともあれ、3で割った余りが等しい2つの数は、大きい方から小さい方を引くと3で割り切れる数になることが分かりましたから、これで証明は終了になります。
まとめると
- ➀4つの正の整数は、3で割った余り毎に分けられる
- ➁そのように分けると、鳩の巣原理から「3で割った余りが同じ2つの数」が（どんな時でも必ず）存在することが分かる
- ③3で割った余りが同じ2つの数同士を引き算すると、結果は3で割り切れる
という流れです。
鳩の巣原理は「どの箱に」「何匹」入っているかまで具体的には分かりませんが、上手く使えば「どれかの箱に2匹以上は入っている」ということまでは断言できます。
なので、具体例を持ってこなくても良い問題、もっと言えば「〇〇が存在することを示せ」というタイプの問題にはこの考え方が滅法効きます。こいつに触れたことがあるのと無いのとでは、発想の手数に差が出ること間違いなしです。
3.おわりに
今回は鳩の巣原理について紹介してきました。理系の受験生に聞いてみると、多くの生徒がこの考え方の存在を知っている一方、文系の生徒には知らない子の方が多く、便利で簡単な考え方だから頭の片隅にでも入れておいてほしい、との思いからこの記事を書くに至りました。
是非覚えて帰ってもらった上で、自分でも（特に書籍などで）調べてみて、活用してみてください。
ところで……実のところを白状してしまえば、本来は今月別の内容を書く予定でした。ところが、調査と執筆が間に合わず、あえなくそいつは来月のテーマとなってしまった、という背景もあります。
先出ししておくと、来月は「読書感想文」のお話をしようと思います。嫌いな夏休みの宿題に挙げる人が多い筆頭格であると認識していますが、実際のところどうなのでしょう。
ちょっと気になったので、読書感想文を嫌う人は多いのか、何故嫌うのか、そもそもどういう意義があって実施されているのか、といったことを一個人に可能な範囲で調査してみようと思います。自分の実体験も織り交ぜるとは思いますが、できるところはデータを活用して話ができると良いかな、と考えています。
それでは、来月もお楽しみに！
