2025年 金沢大学数学(理系)を徹底解説!

皆さんこんにちは。東進衛星予備校 金沢南校の北川と申します。
今月に入り、2025年度の金沢大学前期の入試問題が公式ホームページにて公表されましたので、折角ですから解説記事を作成する運びとなりました[1]。理系の4問について、概観と考え方のポイント、及び解説を掲載いたします。
金沢大学理系を目指す受験生の皆様の参考になれば幸いです。
[1] 予告していたフィボナッチ数列と科学大の問題は、もう既に擦られまくっているので書くとしてももっと後になりそうな気配がしています……。
目次
1.講評
【全体概観】
昨年と比べても易化したと見られます。数学が得意な生徒であれば、時間内に8割程度の得点も狙えるのではないでしょうか。第1問をきっちり確保し、残りの3問のうちから1問を完答、残り2問も半分以上の部分点を狙って動ければ充分でしょう(医学類志望者は満点を目指すつもりで!)。
以下、各問題に関する所感です。難易度は易、やや易、標準、やや難、難の5段階で評価しております(あくまで金大を受験する生徒から見た難易度感です)。
・第1問は図形と方程式、ベクトル、図形の性質などの出題でした。(1)と(2)はよくある問題で、特に苦戦することなく解けるでしょう。(3)もルートによっては計算量が少し多いですが、およそ20分と掛からず得点可能でしょう。やや易で、必ず得点したい問題です。
・第2問は微積分と極限の出題でした。(1)はただ計算するだけで、(2)も定石を知っていればその通り処理できる問題です。(3)は(2)を使える形に変形したり、別の極限値を求めたりとやることは多く、時間内の完答を諦めた方も多いのでは。標準レベルの問題です。
・第3問は誘導なしの回転体の問題。丁寧に図示して正しく場合分けすれば、あとは大したことの無い計算をするだけですが、その正しい場合分けが少し複雑で、どれかを見落とした生徒も多いのではないでしょうか。標準レベルです。
・第4問は整数分野からの出題。(1)は直接計算すれば答えに察しはつくし、(2)も簡単な計算で証明できるのですが、(3)は整数問題に慣れていないと手が止まってしまうかもしれません。完答の難易度ならやや難レベルですが、(2)までは標準レベルなのできっちり得点してほしいところです。
全体概観は以上です。それでは、各問題の解説に入っていきましょう。
2.第1問 解説
第1問はこのような問題でした。
実数 について,座標平面上に3点\(A(1,0),B(m,0),C(m^2,0)\)をとる。点\(P(x,y)\)は\(𝐴𝑃:𝐶𝑃=1:𝑚\)を満たしながら動くとする。次の問いに答えよ。
(1)点\(P(x,y)\)の軌跡を求めよ。
(2)次の等式を証明せよ。
$$\overrightarrow{PB} \cdot \overrightarrow{PC} =m(m+1)(m-x)$$
(3)\(y≠0\)とする。点\(P(x,y)\)に対して\(∠APB=∠BPC\)が成り立つことを示せ。
一部参考書のコラムでも取り上げられることの多い、「アポロニウスの円」に関する問題です。「2定点からの距離の比が常に等しい点の軌跡は円になる」ということで、機械的な計算で証明が可能です。(1)はまさにこの「機械的な計算」を正しく行うだけの問題で、解答は以下の通りです。
(1)点\(P(x,y)\)に対し、\(AP=\sqrt{(1-x)^2+y^2} 、CP=\sqrt{(m^2-x)^2+y^2}\)である。
ここで、\(AP:CP=1:m\)であるから、\(m\sqrt{(1-x)^2+y^2 }=\sqrt{(m^2-x)^2+y^2}\)を得る。
これを計算して整理すると\(x^2+y^2=m^2\)を得る[2]。
以上より、原点中心で半径が\(m\)の円が求める軌跡である。
(2)については、これも\(\overrightarrow{PB}\) と\(\overrightarrow{PC}\) を成分表示して具体的に計算すれば大したことなく計算できます。(1)で得た\(x^2+y^2=m^2\)という関係式も活用して\(y\)を消去することが必要ですが、それほど大した問題ではありません。解答は以下の通りです。
(2) \(\overrightarrow{PB} =(m-x,-y),\overrightarrow{PC} =(m^2-x,-y)\)であるので、
\(\overrightarrow{PB}\cdot\overrightarrow{PC} =(m-x)(m^2-x)+y^2\)
である。ここで、(1)より、点\(P(x,y)\)は\(x^2+y^2=m^2\)という関係式を満たすため、
\((m-x)(m^2-x)+y^2={(m-x)(m^2-x)+m}^2-x^2\)
と変形できる。この式を変形し、
\((m-x)(m^2-x)+m^2-x^2=(m-x)(m^2-x)+(m-x)(m+x)\)
\(=(m-x)(m^2-x+m+x)=(m-x)(m^2-m)=m(m-x)(m-1)\)
を得る。□
(3)は(金沢大学公表の略解を鑑みると)内積と式変形で\(cos∠APB=cos∠BPC\)を求めるのが想定解のようです[3]。ですが、アポロニウスの円が持つ性質から初等幾何的に考察すると、特に難しい式変形もなく証明できてしまうことに気が付いたので、これも別解として載せておきます。
(3) 先ほどと同様に\(\overrightarrow{PA}\cdot\overrightarrow{PB}\)を計算する。\(\overrightarrow{PA}=(1-x,-y)\)であるので、
\(\overrightarrow{PA}\cdot\overrightarrow{PB}=(1-x)(m-x)+y^2=⋯=(m+1)(m-x)\)
が成り立つ。(2)の結果から、\(m\overrightarrow{PA} \cdot\overrightarrow{PB} =\overrightarrow{PA} \cdot\overrightarrow{PC} \)であることが分かる。
内積の定義から、
\(m|\overrightarrow{PA} ||\overrightarrow{PB} |cos∠APB=|\overrightarrow{PB}||\overrightarrow{PC} |cos∠BPC\)
である。一方で、
\(m|\overrightarrow{PA} |=m\sqrt{(1-x)^2+y^2 }=\sqrt{m^2 (1-x)^2+m^2 y^2}\)
\(=\sqrt{m^2-2m^2 x+m^2 x^2+(m^2-1)y^2+y^2}\)
\(=\sqrt{m^2-2m^2 x+m^2 x^2+(m^2-1)(m^2-x^2)+y^2}\)
\(=\sqrt{m^4-2m^2 x+x^2+y^2}\)
\(=\sqrt{(m^2-x)^2+y^2 }=|\overrightarrow{PC} |\)
が分かるので、
\(m|\overrightarrow{PA}||\overrightarrow{PB}|cos∠APB=|\overrightarrow{PB}||\overrightarrow{PC}|cos∠BPC\)
\(|\overrightarrow{PB}||\overrightarrow{PC}|cos∠APB=|\overrightarrow{PB}||\overrightarrow{PC}|cos∠BPC\)
\(cos∠APB=cos∠BPC\)
が分かる。ここで\(∠APB\)と\(∠BPC\)は\(0°\)より大きく\(180°\)より小さい角であるから、
\(∠APB=∠BPC\)
を得る。□
以下が別解です。
(3)[別解] \(AB=m-1,BC=m^2-m=m(m-1)\)であるから、\(AB:BC=1:m\)である。
ところで、問題の条件から\(AP:CP=1:m\)であるから、(\(y≠0\)に注意して)三角形\(APC\)に注目すると、角の二等分線の定理の逆から\(∠APB=∠BPC\)が言える。□
角の二等分線の定理の逆は補助線1本で比較的簡単に証明できるので、その証明まで含めて書いたとしても想定解より短いと思います。ゴリ押し計算で証明するような内容を、図形の性質的観点で素早く解くことができるケースは案外多く、「苦手だから……」「ベクトルとか座標平面があるから……」と避けていると損をするかもしれません。
[2] 本来なら計算過程を省略せず書き、逆も正しいことをチェックした方が良いのかもしれませんが、今回は必要十分な変形しかしていないので逆も正しいのはほぼ明らかと判断して諸々省略しています。計算過程は本番だと省略せず書いた方が良いです。
[3] 実際私も初見ではそうやって解きました。
3.第2問 解説
第2問はこのような問題でした。
実数\(a>0\)に対し,座標平面上の点\(P(a,0)\)をとる。曲線
\(y=\frac{1}{3} x^(\frac{3}{2}) (x≧0)\)
を\(C\)とする。点\(Q\)が曲線\(C\)上を動くとき,\({PQ}^2\)の最小値を与える点\(Q\)の\(x\)座標を\(F(a)\)とし, \({PQ}^2\)の最小値を\(G(a)\)とする。次の問いに答えよ。
(1)\(F(a)\)を求めよ。
(2)\(\lim_\limits{a\to+0}\frac{(F(a)-a)}{a^2 }\)を求めよ。
(3)\(\lim_\limits{a\to+0}\frac{G(a)}{a^3 }\)を求めよ。
まずは(1)からですが、点\(Q\)の座標を適当なパラメータで表して計算していけば、関数の問題として処理できそうだと見当がつきます。実際今回は3次関数というかなり扱いやすい形になり、特に労せずとも解くことができます。解答は以下の通りです。
(1)点Qの座標を(\(t,\frac{1}{3} t^\frac{3}{2}\))とする(\(t≧0\))。このとき、
\(PQ^2=(a-t)^2+(\frac{1}{3}t^\frac{3}{2})^2=\frac{1}{9}t^3+t^2-2at+a^2\)
であり、これを\(t\)についての3次関数として見て、\(t≧0\)における最大値を考えればよい。
\(f(t)=\frac{1}{9}t^3+t^2-2at+a^2\)
とすると、
\(f'(t)=\frac{1}{3} t^2+2t-2a=\frac{1}{3}(t^2+6t-6a)\)
である。\(\frac{1}{3} (t^2+6t-6a)=0\)を解くと、\(t=±\sqrt{9+6a}-3\)であり、\(a\)の範囲から\(\sqrt{9+6a}-3\)は正の実数、\(-\sqrt{9+6a}-3\)は負の実数であることが分かる。以上から、\(f(t)\)の増減表は以下の通り。
| \(t\) | \(0\) | … | \(√(9+6a)-3\) | … |
| \(f'(t)\) | / | – | \(0\) | + |
| \(f(t)\) | \(a^2\) | 減少 | 極小値 | 増加 |
よって、f(t)は極小値をとるときに最小値を取るので、F(a)=√(9+6a)-3。
ここまでは何の変哲もありません。一応、極小値を実際に計算しようとすると地獄のような式になってしまうので、必要がない限りは触れないようにしておきたいと思っておくと良いかもしれません。
次は(2)ですが、具体的に\(F(a)\)が分かっているので代入してみましょう。その後式をグッと睨むと、典型問題としてよく見る「有理化の逆」とされるテクニックを使えば解けそうだと気づきます。後は流れで答案を書けばよく、以下の通りになります。
(3) \(\lim_\limits{a\to+0}\frac{G(a)}{a^3 }=\lim_\limits{a\to+0}\frac{1}{a^3} (\frac{1}{9} F(a)^3+F(a)^2-2aF(a)+a^2 )\)
\(=\lim_\limits{a\to+0}(\frac{1}{9} \cdot\frac{F(a)^3}{a^3} +\frac{F(a)^2}{a^3} -2 \frac{F(a)}{a^2} +\frac{1}{a})\)
\(=\lim_\limits{a\to+0}(\frac{1}{9}\cdot (\frac{(F(a)}{a})^3+\frac{F(a)^2}{a^3} -\frac{F(a)}{a^2} -\frac{F(a)}{a^2}+\frac{1}{a}) \)
\(=\lim_\limits{a\to+0}(\frac{1}{9}\cdot(\frac{F(a)}{a})^3+\frac{F(a)}{a}(\frac{F(a)-a}{a^2})-(\frac{F(a)-a}{a^2}))\)
ここで、 \(\lim_\limits{a\to+0} \frac{F(a)}{a}=\lim_\limits{a\to+0}\frac{\sqrt{9+6a}-3}{a}\)
\(=\lim_\limits{a\to+0} \frac{(\sqrt{9+6a}-3)(\sqrt{9+6a}+3)}{a(\sqrt{9+6a}+3)}\)
\(=\lim_\limits{a\to+0} \frac{9+6a-9}{a(\sqrt{9+6a}+3)}=\lim_\limits{a\to+0} \frac{6}{(\sqrt{9+6a}+3)}=\frac{6}{(\sqrt{9+3})}=1\)
であるから、
\(=\lim_\limits{a\to+0} (\frac{1}{9}\cdot(\frac{F(a)}{a})^3+\frac{F(a)}{a}(\frac{F(a)-a}{a^2})-(\frac{F(a)-a}{a^2})\)
\(=\frac{1}{9}\cdot1+1\cdot(-\frac{1}{6})-(-\frac{1}{6})=\frac{1}{9}\)
である。
以上より、\(=\lim_\limits{a\to+0}\frac{G(a)}{a^3}=\frac{1}{9}\)
なんとか(2)を使える形にならないかな~と考えると、\(2 \frac{F(a)}{a^2}を\frac{F(a)}{a^2}+\frac{F(a)}{a^2}\)に分解する発想が出てきたり、\(\frac{F(a)}{a}\)の極限を求めようという発想になったりするのではないかと思います。
4.第3問 解答
続いて第3問は以下のような問題でした。
座標平面上の\(0≦x≦2log2\)の範囲において,曲線\(y=e^x\)と曲線\(y=2-e^{2x}\),直線\(x=2log2\)で囲まれた図形を\(D\)とする。図形\(D\)を\(x\)軸の周りに1回転してできる回転体の面積\(V\)を求めよ。
とりあえず図示して、とりあえず範囲を求めて、とりあえず計算するだけなのですが、それらを「とりあえず」やるのが大変な問題です。
チェックポイントとしては以下のような感じでしょうか。
・グラフの概形を図示する
・回転体の体積が\(\frac{1}{2} log2\)までで一旦区切れることを確認する
・\(\frac{1}{2} log2\)から\(log2\)までと、\(log2\)から\(2log2\)までで積分する関数が変わることを確認する
・実際に計算する
特に「確認する」2つがかなり面倒で、途中でミスをする可能性はかなり高いです。丁寧に1つ1つ解いていきましょう。
解答は以下の通りです。
\(y=2-e^{2x}\)を\(x\)について微分すると\(y’=-2e^{2x}\)であり、これはすべての実数\(x\)について負の値を取るから、\(y=2-e^{2x}\)は定義域全体で単調減少である。
また、\(2-e^{2x}=0\)を解くと\(x=\frac{1}{2}log2\)であり、これを基にグラフの概形を図示すると下図の通りである。下図の赤く塗った部分を\(x\)軸周りに回転させたときの立体の体積を求めればよい。
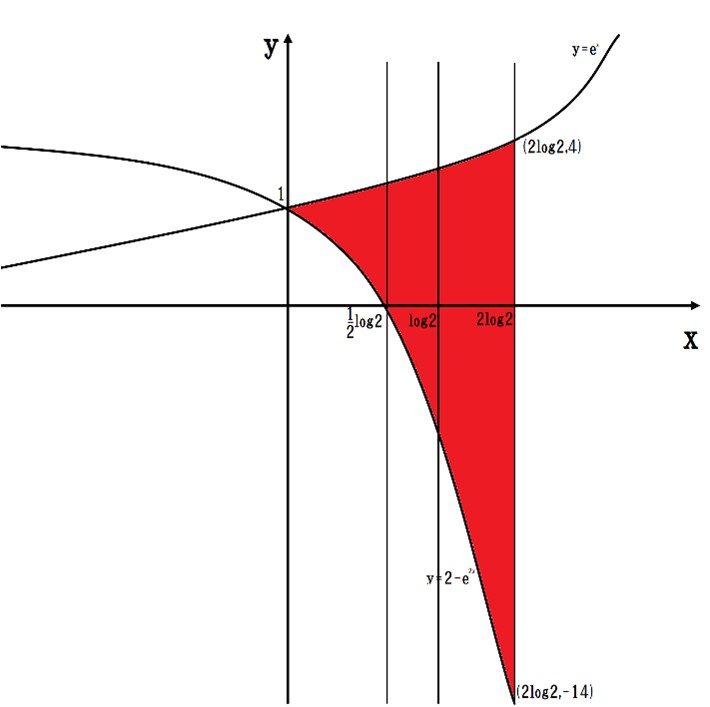
ここで、不等式\(|2-e^{2x} |<|e^x |\)を解くと、\(0<x<log2\)が分かる。
よって、回転体の断面は
・\(0≦x≦\frac{1}{2} log2\)においては半径\(|e^x |\)の円から半径\(|2-e^{2x} |\)の円をくり抜いた図形
・\(\frac{1}{2} log2<x≦log2\)においては半径\(|e^x |\)の円
・\(log2<x<2log2\)においては半径\(|2-e^2x |\)の円
になっていることが分かる。従って、求める面積は
\(V=π\int_0^{\frac{1}{2}log2}((e^x)^2-(2-e^{2x})^2)dx+π\int_{\frac{1}{2}log2}^{log2} (e^x)^2 dx+π\int_{log2}^{2log2}(2-e^{2x})^2 dx\)
であり、これを計算して[4]
\(V=(\frac{7}{4}-2log2)π+π+(36+4log2)π=2πlog2+\frac{155}{4 }π\)
を得る。
焦らず、正しく素早く計算できたでしょうか?
ほとんどが\(e\)に関する積分なので計算自体はそれほど難しくはないのですが、分量がやや多く、自身の計算力に対する信頼が問われます。
[4] 本番ではある程度計算過程を書いた方が良いと思いますが、今回は省略します。
5.第4問 解説
さて、最後の第4問は以下のような問題でした。
次の式によって与えられる数列\(\{a_n\},\{b_n\},\{x_n\}\)がある。
\(a_n=\displaystyle \sum_{k=1}^n k ,b_n=\displaystyle\sum_{k=1}^n k^2 ,x_n=\displaystyle\sum_{k=1}^n ka_k \)
次の問いに答えよ。
(1)\(\frac{b_n}{a_n}\)が整数となる\(n\)をすべて求めよ。
(2)\(x_n=\frac{1}{2}({a_n}^2+b_n)\)を示せ。
(3)\(\frac{x_n}{a_n}\)が整数となる\(n\)をすべて求めよ。
恐らく、受験勉強の中で3乗和の公式までは覚えているでしょうから、それを使えば(2)まではそれほど苦も無く解けるのではないでしょうか。解答は以下の通りです。
(1)\(a_n=\frac{1}{2} n(n+1) ,b_n=\frac{1}{6} n(n+1)(2n+1)\)であるので、
\(\frac{b_n}{a_n}=\frac{1}{3}(2n+1)\)
だと分かる。これが整数になることは\(2n+1≡0(mod3)\)と同値。また、\(n\)を\(3\)で割った余りで分類すると、
・\(n≡0(mod3)\)のとき、\(2n+1≡1(mod3)\)
・\(n≡1(mod3)\)のとき、\(2n+1≡0(mod3)\)
・\(n≡2(mod3)\)のとき、\(2n+1≡2(mod3)\)
であるから、\(2n+1≡0(mod3)\)は\(n≡1(mod3)\)と同値である。
以上より、\(n≡1(mod3)\)を満たすすべての正の整数\(n\)が答えである。
(2)\( x_n=\sum_{k=1}^n ka_k = \sum_{k=1}^n k\cdot \frac{1}{2} k(k+1)\)
\(= \frac{1}{2} \sum_{k=1}^n (k^3+k^2) = \frac{1}{2}(\sum_{k=1}^n k^3+\sum_{k=1}^n k^2 )\)
ここで、
\( \displaystyle \sum_{k=1}^n k^3 =(\frac{1}{2} n(n+1))^2={a_n}^2\)
\( \displaystyle \sum_{k=1}^n k^2 =b_n \)
であるので、
\(x_n=\frac{1}{2}(\displaystyle \sum_{k=1}^n k^3+ \displaystyle \sum_{k=1}^n k^2 ) = \frac{1}{2}({a_n}^2+b_n)\)
が得られる。□
問題の(3)については、\(a_n\)や\(b_n\)が残ったままの形だと考察しづらいので、\(n\)の多項式で表すことで考察が進みます。後は12で割った剰余を上手に考えられるかどうか……4で割った余りと3で割った余りを別々に考えればよいということを、確信を持って思いつけたかどうかにかかっているでしょう(背景として中国剰余定理を知っていればそう難しくなかったかも?)。
(3)(2)より、
\(\frac{x_n}{a_n}=\frac{1}{2a_n} ({a_n}^2+b_n )\)
\(=\frac{1}{2}(a_n+\frac{b_n}{a_n})\)
\(=\frac{1}{2} (\frac{1}{2}n(n+1)+\frac{1}{3}(2n+1))\)
\(=\frac{1}{12}({3n}^2+7n+2)\)
\(=\frac{1}{12}(3n+1)(n+2)\)
以上より、これが整数になることは\((3n+1)(n+2)≡0(mod12)\)と同値。ここで\(12=3×4\)であり、\(3\)と\(4\)は互いに素であるから、\((3n+1)(n+2)≡0(mod12)\)は「\((3n+1)(n+2)≡0(mod3)\)かつ\((3n+1)(n+2)≡0(mod4)\)」と同値であることに注意する。
○\((3n+1)(n+2)≡0(mod3)\)は、\(3n+1\)がいかなる整数\(n\)についても\(3\)の倍数にならないことから、\(n+2≡0(mod3)\)、つまり\(n≡1(mod3)\)と同値。
○\((3n+1)(n+2)≡0(mod4)\)は、\(n\)を\(4\)で割った剰余で分類すると、
・\(n≡0(mod4)\)のとき、\((3n+1)(n+2)≡1\cdot2≡2(mod4)\)
・\(n≡1(mod4)\)のとき、\((3n+1)(n+2)≡0\cdot3≡0(mod4)\)
・\(n≡2(mod4)\)のとき、\((3n+1)(n+2)≡3\cdot0≡0(mod4)\)
・\(n≡3(mod4)\)のとき、\((3n+1)(n+2)≡2\dot1≡2(mod4)\)
となるので、\((3n+1)(n+2)≡0(mod4)\)は\(n≡1(mod4)\)または\(n≡2(mod4)\)と同値。
つまり、\((3n+1)(n+2)≡0(mod12)\)は「”\(n≡1(mod3)\)かつ\( n≡1(mod4)\)”または”\( n≡1(mod3)\)かつ \(n≡2(mod4)\)”」と同値。
ここで、
・\(n≡1(mod3)\)かつ\( n≡1(mod4)\)は\(n≡1(mod12)\)と同値。
・\(n≡1(mod3)\)かつ \(n≡2(mod4)\)は\(n≡10(mod12)\)と同値。
であるので、結局\((3n+1)(n+2)≡0(mod12)\)は「\(n≡1(mod12)\)または\(n≡10(mod12)\)」と同値であると分かる。
以上より、求める答えは\(n≡1(mod12)\)または\(n≡10(mod12)\)となるようなすべての正の整数\(n\)である。
とても長いですね……。
6.終わりに
さて、どうでしたでしょうか?
金沢大学は難関大学として分類されることも多い大学です。たびたび「最低限、金大ぐらいは合格したい」と言っている方もいらっしゃいますが、その「最低限金大に合格できる学力」とは、上記の問題に対して7~8割得点できる学力のことです。そこは決して、誰もが簡単に辿り着ける場所ではありません。
問題の理解、正確な計算、使える手筋の多さと状況に合わせた的確な判断、これらが全部そろって初めてスタートラインです。しかも、数学だけに限らず、理科や英語も2次試験で問われますし、共通テストでは国語や情報、社会も問われます。これらすべてを攻略するためのかなりハードな対策の果てに、ようやく合格点に辿り着く人が大半です。
全員がこの対策を完璧に、余裕をもってこなせるとは限りません。
では、ハードな対策を少しでも余裕をもって行うにはどうすればよいでしょうか?
1つの答えとしては、受験生は少しでも効率を上げる(質の向上)こと、非受験生は今から受験勉強を意識して対策を始める(量の向上)ことが挙げられるでしょう。質と量、2つの対策を頑張って、各々の春に合格をつかみ取りましょう!
今月はここまで。来月の記事もお楽しみに!




